投资需要有显微镜、放大镜、望远镜。小到具体的产品细节，大到财务会计分析，现金流折现，各种估值，再到宏观的公司战略与“护城河”研究，甚至宏观经济与国际政治经济。

但是，这些镜子虽然是在不同的范畴内看问题，视角虽然远近不同，但没有本质的区别。如果你有钓鱼的经验，就会知道偏振光镜的妙用。水面的反光会让人看不清水下的鱼，但是偏振镜会过滤掉水面反光，让你看到水面下的鱼。这就是一个截然不同的视角的作用。而统计分析就是这样一个不同的视角，就好像是投资者的“偏振镜”。

说到统计，曾经是我大学时最头痛的课程。但是现在看来，我要感谢我的教授，“四大名捕”之一，让我在离开校园后很久还能熟练的理解统计分析的基本原理，并加之运用。

大数定律

辩证法认为偶然中蕴含着必然。统计就是从偶然中发现必然的学问。在随机事件的大量重复出现中，往往呈现几乎必然的规律，这个规律就是大数定律。通俗地说，这个定理就是，在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。比如，我们向上抛一枚硬币，硬币落下后哪一面朝上本来是偶然的，但当我们上抛硬币的次数足够多后，达到上万次甚至几十万几百万次以后，我们就会发现，硬币每一面向上的次数约占总次数的二分之一。偶然必然中包含着必然。

大数定律有很多种：

1. 切比雪夫大数定律

设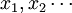是一列两两相互独立的随机变量，服从同一分布，且存在有限的数学期望a和方差σ²，则对任意小的正数ε，有：

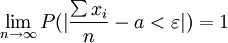
该定律的含义是：当n很大，服从同一分布的随机变量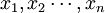的算数平均值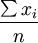将依概率接近于这些随机变量的数学期望。

随着样本容量n的增加，样本平均数将接近于总体平均数。从而为统计推断中依据样本平均数估计总体平均数提供了理论依据。正因为有了这个定律，统计才有了意义，因为就可以通过采样推断全体。

2. 贝努里大数定律

大学时，这个定律被戏称作“白努力”定律。

设μ_n是n次独立试验中事件A发生的次数，且事件A在每次试验中发生的概率为P，则对任意正数ε，有：

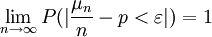
该定律是切贝雪夫大数定律的特例，其含义是，当n足够大时，事件A出现的频率将几乎接近于其发生的概率，即频率的稳定性。在抽样调查中，用样本去估计总体，其理论依据即在于此。抽样调查的全部基础就是这个定律。

中心极限定理

大数定律揭示了大量随机变量的平均结果，但没有涉及到随机变量的分布的问题。而中心极限定理说明的是在一定条件下，大量独立随机变量的平均数是以正态分布为极限的。

中心极限定理是概率论中最著名的结果之一。它提出大量的独立随机变量之和具有近似于正态的分布。因此，它不仅提供了计算独立随机变量之和的近似概率的简单方法，而且有助于解释为什么有很多自然群体的经验频率呈现出钟形(即正态)曲线这一事实，因此中心极限定理这个结论使正态分布在数理统计中具有很重要的地位，也使正态分布有了广泛的应用。

正因为有了大数定律和中心极限定理，我们才可以从统计分析这样一个完全不同的视角看问题。比如，住房的租售比多少算高？仅仅看绝对数，谁也说不好。但是，转换成统计分析的标准方差Sigma，任何一个有着统计基础的人都会告诉你4.5个Sigma意味着什么。

（本文参考了MBA智库百科网站）