根据美国国家闪电安全协会(National Lightning Safety Istitute)统计，美国人口2.8亿左右，每年有约1000人受到闪电伤害。因此在美国，一个人被闪电击中的概率是1/280,000=0.00035714%左右。

Sigma就是标准差，在概率统计中最常使用做为统计分布程度（statistical dispersion）上的测量。标准差定义为方差的算数平方根，反映组内个体间的离散程度。

在实际应用上，常考虑一组数据具有近似于正态分布的机率分布。若其假设正确，则约 68% 数值分布在距离平均值有 1个标准差之内的范围，约 95% 数值分布在距离平均值有 2 个标准差之内的范围，以及约 99.7% 数值分布在距离平均值有 3个标准差之内的范围。称为 "68-95-99.7 rule"。

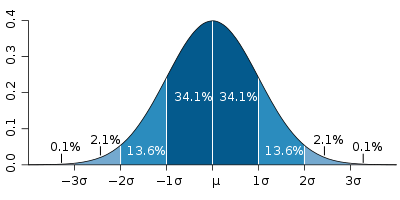
在正态分布的几率中，超过1个Sigma的事件的概率大约是15.8%左右，而超过3个Sigma的概率大约是0.1%左右。被闪电击中的概率大约是4.5个Sigma左右。日本泡沫高峰时60倍的租售比就相当于4.5个Sigma的事件。而租售比超过60的几率就小于被闪电击中的概率。

泡沫极度膨胀的概率虽然低，但仍然会发生。总有人会被雷劈死。泡沫为什么会破？因为价格再往上走的概率比被雷劈死的概率还要小。这是不可能的，价格只能下跌，恢复正常。这就是Sigma的威力，这就是自然界的规律。